ক্যালকুলাস হল গণিতের একটি শাখা যা পরিবর্তন এবং গতি নিয়ে কাজ করে। এটি প্রধানত দুইটি গুরুত্বপূর্ণ অংশে বিভক্ত:

1. ডিফারেনশিয়াল ক্যালকুলাস (Differential Calculus) – এটি পরিবর্তনের হার (Rate of Change), কোন ফাংশনের স্পর্শক (Tangent) এবং ঢাল (Slope) বের করতে ব্যবহৃত হয়। যেমন, একটি গাড়ির গতি (Speed) পরিবর্তন হলে, ক্যালকুলাস ব্যবহার করে আমরা তার ত্বরণ (Acceleration) নির্ণয় করতে পারি।

2. ইন্টেগ্রাল ক্যালকুলাস (Integral Calculus) – এটি ক্ষেত্রফল (Area), আয়তন (Volume) এবং মোট পরিবর্তন (Total Accumulation) বের করতে ব্যবহৃত হয়। যেমন, যদি আমরা জানি একটি গাড়ি কীভাবে চলছে, তাহলে ইন্টেগ্রাল ক্যালকুলাস ব্যবহার করে মোট দূরত্ব নির্ণয় করতে পারি।

সহজ উদাহরণ

ধরো, তুমি পাহাড়ে উঠছো।

• ডিফারেনশিয়াল ক্যালকুলাস বলবে, তুমি যে মুহূর্তে আছো, সেই মুহূর্তে তোমার চলার গতি কত (Slope)।
• ইন্টেগ্রাল ক্যালকুলাস বলবে, পুরো পথ ধরে তুমি মোট কত উচ্চতায় উঠলে (Total Area)।

বাস্তব জীবনে ক্যালকুলাসের ব্যবহার

• পদার্থবিদ্যায় গতির বিশ্লেষণে
• অর্থনীতিতে লাভ-ক্ষতির হিসাব করতে
• কম্পিউটার গ্রাফিক্স এবং মেশিন লার্নিংয়ে
• ইঞ্জিনিয়ারিং এবং স্থাপত্যে কাঠামোর ডিজাইন করতে

ক্যালকুলাস হল পরিবর্তন এবং জমা নিয়ে কাজ করার একটি শক্তিশালী গণিতীয় হাতিয়ার। ডিফারেনশিয়াল ক্যালকুলাস পরিবর্তনের হার পরিমাপ করে, যখন ইন্টিগ্রাল ক্যালকুলাস জমা বা সমষ্টি পরিমাপ করে। এই দুটি ধারণা একসাথে কাজ করে বিজ্ঞান, প্রকৌশল, অর্থনীতি, এবং আরও অনেক ক্ষেত্রে জটিল সমস্যার সমাধান করে।

১. ডিফারেনশিয়াল ক্যালকুলাস (Differential Calculus)

ডিফারেনশিয়াল ক্যালকুলাস পরিবর্তনের হার নিয়ে কাজ করে। এটি কোন ফাংশনের স্পর্শক (Tangent) এবং ঢাল (Slope) নির্ধারণ করতে সাহায্য করে।

ডেরিভেটিভ (Derivative)

ডেরিভেটিভ হল ডিফারেনশিয়াল ক্যালকুলাসের মূল ধারণা। এটি একটি ফাংশনের পরিবর্তনের হার পরিমাপ করে। যদি y=f(x) হয়, তাহলে y এর সাপেক্ষে x এর ডেরিভেটিভ dy/dx​ বা f′(x) দ্বারা প্রকাশ করা হয়। উদাহরণ:

• যদি f(x)=x2 হয়, তাহলে f′(x)=2x ।
• এখানে f′(x) হল f(x) এর ঢাল, অর্থাৎ x এর মান পরিবর্তনের সাথে f(x) কত দ্রুত পরিবর্তন হচ্ছে তা নির্দেশ করে।

প্রয়োগ:

• গতি এবং ত্বরণ: যদি s(t) সময় t এর সাথে একটি বস্তুর অবস্থান নির্দেশ করে, তাহলে ds/dt হল বস্তুর গতি এবং d2s/dt2 হল ত্বরণ।
• অর্থনীতিতে সীমান্তিক খরচ এবং সীমান্তিক আয়।

২. ইন্টিগ্রাল ক্যালকুলাস (Integral Calculus)

ইন্টিগ্রাল ক্যালকুলাস জমা বা সমষ্টি নিয়ে কাজ করে। এটি কোন ফাংশনের অধীনে এলাকা পরিমাপ করতে এবং বিভিন্ন জমা প্রক্রিয়া বোঝাতে ব্যবহৃত হয়। প্রয়োগ:

• এলাকা এবং আয়তন নির্ণয়: কোন বক্ররেখার অধীনে এলাকা বা ঘূর্ণনের মাধ্যমে সৃষ্ট আয়তন নির্ণয়।
• পদার্থবিজ্ঞানে কাজ এবং শক্তি: কোন বল দ্বারা কৃত কাজ পরিমাপ করতে ইন্টিগ্রাল ব্যবহার করা হয়।

৩. ডিফারেনশিয়াল এবং ইন্টিগ্রাল ক্যালকুলাসের সম্পর্ক

ডিফারেনশিয়াল এবং ইন্টিগ্রাল ক্যালকুলাস একে অপরের বিপরীত প্রক্রিয়া। এটি ফান্ডামেন্টাল থিওরেম অফ ক্যালকুলাস দ্বারা ব্যাখ্যা করা হয়।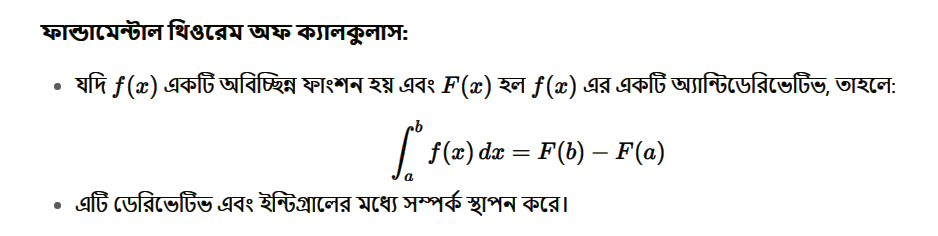  

বাস্তব উদাহরণের মাধ্যমে ক্যালকুলাস বিশ্লেষণ

ক্যালকুলাস আমাদের চারপাশের বাস্তব জীবনের অনেক সমস্যার সমাধান করে। এখানে আমরা কয়েকটি বাস্তব উদাহরণ দিয়ে ক্যালকুলাসের গুরুত্ব বিশ্লেষণ করব।

---

১. গাড়ির গতি ও ত্বরণ (Speed & Acceleration) – ডিফারেনশিয়াল ক্যালকুলাস

পরিস্থিতি:

ধরো, তুমি একটা গাড়ি চালাচ্ছো। তুমি স্পিডোমিটারে দেখলে গাড়ির গতি প্রতি সেকেন্ডে ১০ মিটার থেকে বেড়ে ১৫ মিটার হয়ে যাচ্ছে।

ক্যালকুলাসের বিশ্লেষণ:

বাস্তব প্রয়োগ:

• গাড়ির ব্রেকিং সিস্টেম ডিজাইন
• রেসিং কারের গতি নিয়ন্ত্রণ

---

২. ভবনের ছাদে জল জমা হওয়া – ইন্টেগ্রাল ক্যালকুলাস

পরিস্থিতি:

একটি ভবনের ছাদ বৃষ্টির জল সংরক্ষণ করে। আমরা জানতে চাই, এক ঘণ্টায় ছাদে কত লিটার জল জমেছে?

ক্যালকুলাসের বিশ্লেষণ:

• বৃষ্টিপাতের হার যদি $r(t)$ হয়, তাহলে মোট জমা হওয়া জল বের করতে ইন্টিগ্রাল ক্যালকুলাস ব্যবহার করা হয়।
• যদি বৃষ্টিপাতের হার হয় r(t)=3+2t লিটার/ঘণ্টা, তাহলে মোট জল:

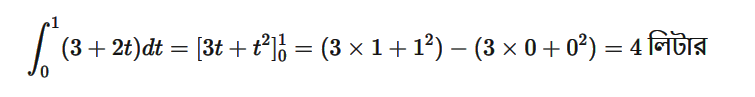
বাস্তব প্রয়োগ:

• ড্যাম বা জলাধারে জল সংরক্ষণ হিসাব
• কৃষি ক্ষেত্রে সেচ ব্যবস্থাপনা

---

৩. ওষুধের শরীরে ক্রিয়া – ডিফারেনশিয়াল ও ইন্টেগ্রাল ক্যালকুলাস

পরিস্থিতি:

একজন রোগীকে একটি ওষুধ দেওয়া হলো। আমরা জানতে চাই, ওষুধ কীভাবে রক্তে ছড়িয়ে পড়বে এবং কতক্ষণ কার্যকর থাকবে?

ক্যালকুলাসের বিশ্লেষণ:

• ওষুধ গ্রহণের পর, তার রক্তে শোষণের হার ডিফারেনশিয়াল ক্যালকুলাস দিয়ে বের করা হয়।
• এক্সপোনেনশিয়াল ফাংশনের সাহায্যে ওষুধের মাত্রা 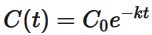 হিসেবে নির্ধারণ করা হয়।
• ওষুধের মোট কার্যকারিতা বোঝার জন্য ইন্টেগ্রাল ক্যালকুলাস দিয়ে বিশ্লেষণ করা হয়।

বাস্তব প্রয়োগ:

• চিকিৎসা ক্ষেত্রে ওষুধের ডোজ নির্ধারণ
• টিকা কার্যকারিতার বিশ্লেষণ

---

৪. ব্যাঙ্কের সুদ গণনা – ইন্টেগ্রাল ক্যালকুলাস

পরিস্থিতি:

তুমি ব্যাংকে ১০,০০০ টাকা রেখেছো, যা বার্ষিক ৫% সুদে জমবে। তুমি জানতে চাইছো, ১০ বছরে কত টাকা হবে?

ক্যালকুলাসের বিশ্লেষণ:

• চক্রবৃদ্ধি সুদ হিসাব করতে ক্যালকুলাস ব্যবহার করা হয়।
• যদি সুদের হার $r$ হয়, তাহলে মোট টাকা:

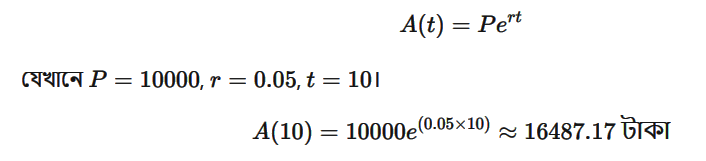
বাস্তব প্রয়োগ:

• বিনিয়োগ এবং স্টক মার্কেট বিশ্লেষণ
• ঋণের সুদ হিসাব

---

৫. ইন্টারনেটের স্পিড অপটিমাইজেশন – ডিফারেনশিয়াল ক্যালকুলাস

পরিস্থিতি:

ইন্টারনেট ব্যবহার করার সময়, ব্রাউজারের পেজ লোড হতে দেরি হয়। কোম্পানি চায়, কীভাবে লোডিং টাইম কমানো যায়।

ক্যালকুলাসের বিশ্লেষণ:

• সার্ভার রেসপন্স টাইম এবং ব্যান্ডউইডথ ব্যবহার ডিফারেনশিয়াল ক্যালকুলাস দিয়ে বিশ্লেষণ করা হয়।
• কোন প্যারামিটার পরিবর্তন করলে পেজ লোডিং দ্রুত হবে, তা বের করতে ডেরিভেটিভ ব্যবহার করা হয়।

বাস্তব প্রয়োগ:

• গুগল, ইউটিউব, নেটফ্লিক্সের লোডিং স্পিড অপটিমাইজেশন
• মোবাইল নেটওয়ার্ক অপটিমাইজেশন